
Siddhant Bansal
Indian Institute of Technology, Gandhinagar
siddhant2697@gmail.com
This is a web page dedicated to the work done by me at IIT Gandhinagar.
Creation of a pipeline that takes in 3D point clouds and gives out a complete 3D geometric model is a pretty vast topic which includes various currently focused research concepts like Rigid and Non-Rigid Point Cloud Registration, 3D object recognition, and Point Cloud Completion. These generated 3D models find various applications in the domain of 3D Computer Vision, 3D Graphics, architecture simulation, games graphics, animated movies, 3D documentation of objects, and many other renowned fields. This research project aims at using various digital geometry processing approaches for preserving and restoring cultural heritage.
Task here is to develop an end-to-end pipeline which begins with acquisition of 2.5D point clouds using a long-range laser scanner. It is followed by point cloud registration to obtain a complete 3D point cloud. If the point cloud is incomplete then applying point cloud completion algorithms for completing the point clouds. The complete point clouds are then converted to mesh, the mesh is then converted to surface. Finally a complete 3D model is obtained which can be 3D printed. My work was focused on understanding and applying various point cloud registration and completion methods.
Geometry Processing is involved with the efficient acquisition, representation, optimization, editing, and simulation of geometric objects. There is a large boost in the availability of 3D data due to the decreasing prices of geometry acquisition devices, like 3D laser scanners (Fig.1), LiDAR (Light Detection and Ranging) scanners. Geometry processing is playing an important role in a large range of applications. Examples include video games, animation, TV, building design, web design, CAD, interactive shape editing, simulations for medical applications and movie productions[1]. Problems arising in these highly diverse fields follow the same fundamental geometry principles proves geometry processing to be a potentially growing field of high potential impact research[2].

Fig.1: 3D Laser scan (Point Cloud) of our lab at IIT Gandhinagar
For converting a point cloud (Fig.1) to a usable 3D model various steps are to be performed. The entire pipeline is explained in Section 2 with all the experiments done. Section 3 covers extra information of stuff did at the internship. Section 4 concludes the discussion with possible future work.
The task of the following pipeline is to convert a less usable point clouds to more usable complete 3D models.
Data acquisition is the process of converting a signal measuring real physical condition to a digital signal that can be manipulated by a digital computer[3]. For our purpose of collecting 3D data, we used the FARO Focus 3D X 330 HRD[4] long-range laser scanner (Fig.2). It is a portable laser scanner capable of taking scans up to 330 meters. The laser scanner throws a laser beam on to the object and calculates how long it takes the laser beam to bounce back from the surface and return. This is how the distance of the object from the laser scanner is calculated and the point cloud is constructed[5].
Fig.3 shows the basic structure of a 3D laser scanner. The mirror rotates on its axis to form a 3D scan of the surroundings The tripod is used to keep the scanner stable while scanning. And it has various indicator lights for indication various operations (their function changes with various manufacturers).
Fig.1 is an example of a point cloud obtained using Faro Focus 3D X 330 HDR scanner.
As it can be seen in Fig.1, a single scan of an object does not contain entire information of the object. There are some missing places in the final single scan of the object. This is a well-known issue and plays an essential role in many practical applications, such as 3D reconstruction and mapping, object pose estimation, LiDAR SLAM and others. To overcome this issue more than one scan of an object is obtained from different orientations. Then all the scans are stitched together to form the true 3D scan of the object. In order to perform the 'stitching' various algorithms are used. These algorithms are used to estimate the relative transformation (a combination of rotation and translation) between the point clouds.
The most common method is the Iterative Closest Point (ICP)[6] algorithm for solving the point cloud registration problem. It works by estimating point correspondences and performing least-squares optimization. There are several versions of the ICP available, we used the one defined by [6]. Using ICP we wish to find a rigid transformation that optimally aligns the two sets in the least-squares sense[7].
We seek to find a Rotation R and translation vector t such that
where wi > 0 are weights for each point pair.
Now the steps are as follows[7]:
The above steps are repeated until an optimal result is obtained. We implemented the above algorithms in Python and obtained the following results on a chair and bunny data set. The code developed is available here https://github.com/Sid2697/3D.

Fig.4: ICP application on chair

Fig.5: ICP application on bunny
The data collected from 3D scanners are often incomplete which leads to a loss in semantic and geometric information. For example, as shown in Fig.6 the cars in the LiDAR scan are barely recognizable as the data points are very sparse due to sensor resolution and occlusion.
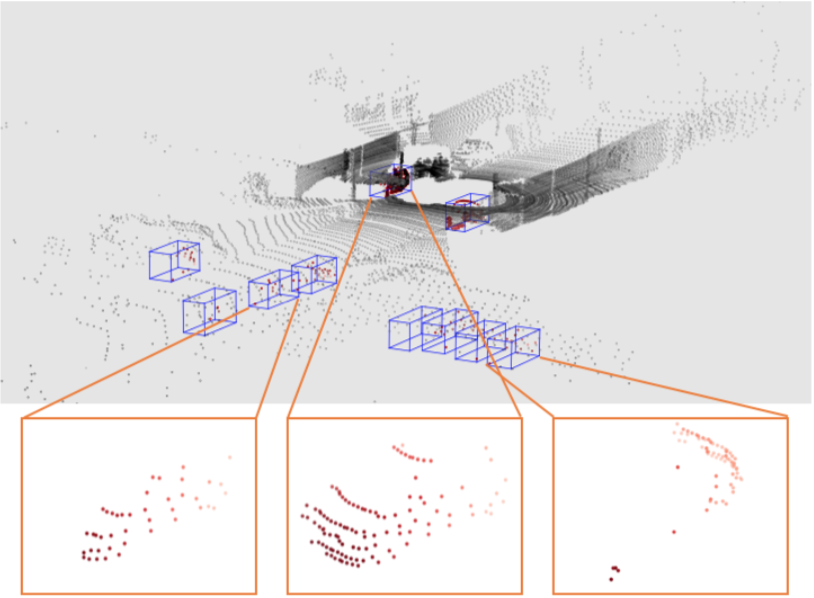
Fig.6: Cars are hardly recognisable due to sparsity of data (source)
The task here is to predict the full shape of the object from the incomplete scan as shown in Fig.6 acquired by LiDAR. This leads to applications like scene understanding, robot manipulation, and manipulation of completed shapes. Previous works like [9] include encoder-decoder network, here the encoder encodes the input to embedding, and the decoder generates the point cloud from the embedding. [8] learn to generate point cloud as manifold using a series of folding operations on the Euclidean plane. [10] assume the point clouds of the 3D object is on a 2-manifold space that locally resembles the Euclidean plane. The decoder proposed by them learns a set of deformations from euclidean plane to the object point cloud.
Going through all the methods like PCN [8], AtlasNet [10], Scan2Mesh [11], and TopNet [12] I wondered what will happen if we try an encoder-decoder architecture consisting of only fully-connected layers. So, I designed an auto-encoder with all the fully-connected layers and no convolution layers. The code developed is available here https://github.com/Sid2697/Fill_missing. The architecture of the encoder was as follows it consisted of fully-connected layers which took 2048 cloud points as input and decreased it to 1024 -> 512 -> 256 -> 128 -> 64. In this manner an encoded code with 64 points was obtained which was further feed into the decoder which would up-sample it back to 2048 points by 64 -> 128 -> 256 -> 512 -> 1024 -> 2048. In this way, a point cloud smaller in size and with more shape information was retrieved. Fig.7 shows the architecture.
Fig.7 Architecture of the auto-encoder designed. Here n represents the batch size while training. The encoder takes in n point-clouds of shape (3, 2048) and creates a code of shape (n, 3, 64). The decoder takes this code and up-samples it create the point-clouds of the original shape.
The data set used for training was obtained from here.
Two types of losses were used to train the network (in two different experiments). First Euclidean distance was used, and in the second one, Chamfer distance[13] was used. Fig.8 shows results obtained using Euclidean distance. Fig.9 shows the results using Chamfer distance[13].
Fig.8 Results using Euclidean distance, the network is not able to generalize on the shapes well and not able to get a sense of the global shape of the point cloud. But it still gives decent shapes despite simple execution.
Fig.9 Results using Chamfer distance, here it can be seen the network is learning much better as compared to Euclidean distance. The network seems to learn the global structure from the input shapes.
The above two experiments concluded that we can use a simple fully-connected linear neural network to solve a complex problem like cloud completion. Out of the two loss functions used Chamfer distance proved to be a better one (by visual inspection of the results). Whereas Euclidean distance proved to be more computationally easy to compute. Although the above experiments did not yield the desired results, this attempt was proof that we can use simple fully-connected neural networks for cloud completion task. If successful they will prove to be very useful for applications using less computational resources like robots using Raspberry Pi.
For the construction of a surface joining the points in the point-cloud is necessary. One possible way of connecting all the points in the point cloud is to form n number of triangles by connecting the points. Out of many, we will discuss two types of possible triangulations techniques[14]:
The idea behind random triangulation is, a point from the set is chosen at random from which the point under consideration can be connected. This pair of point is connected forming a new edge. This process is repeated until all the points are connected. Fig.10 shows connections made using random triangulation.
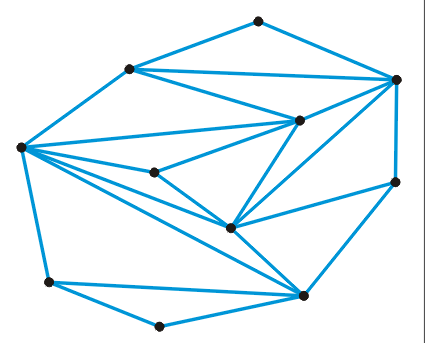
Fig.10 Triangulation done using Random Triangulation process (source)
The advantage of using this process is that it provides uniform triangulation, and tries to get a larger number of equilateral triangles. Conditions to fulfill for successful application of Delaunay triangulation is all the edges must be 'legal edges' (edges belonging to the convex hull of the set of points). Fig.11 shows connections made using Delaunay triangulation.
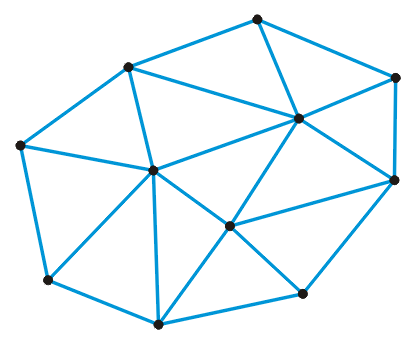
Fig.11 Triangulation done using Delaunay Triangulation process (source)
During the internship, I read a couple of books and a dozen papers. The books helped me in
understanding the concepts better and get a mathematical insight into the 3D geometry world.
List of books I read is
as follows:
List of papers read with summaries written by me is as follows:
I have presented a pipeline to the generation of complete 3D models from point cloud collected using a laser scanner. The pipeline consisted of various sections like data acquisition, point cloud registration, point cloud completion, and triangulation. All these processes help convert a point cloud to a complete 3D model. A new approach was tried in point cloud completion which showed potential in the application of fully-connected linear auto-encoders for the point cloud generation. This work can be carried on and improved to compete with the state-of-the-art results.
I would like to express my gratitude towards my guide Dr. Shanmuganathan Raman
for his timely support and guidance.
I also owe my deep gratitude towards Dr. Rajendra Nagar for his discussions and
Nayan Chaudhary for his support with the experiments.